آموزش برنامه نویسی متلب – مرور توابع و مفاهیم

برنامه نویسی متلب
متلب زبانی بسیار قدرتمند برای حل مسائل گوناگون مهندسی و علمی است. این زبان با داشتن انبوهی از جعبه ابزارهای گوناگون، تقریبا هر کاری را در زمینه برنامه نویسی مهندسی امکانپذیر می سازد. علاوه بر این، سادگی برنامه نویسی به زبان متلب، موجب بکارگیری آن در شاخه ها و گرایش های مختلف علمی شده است.

برنامه نویسی متلب
متلب زبانی بسیار قدرتمند برای حل مسائل گوناگون مهندسی و علمی است. این زبان با داشتن انبوهی از جعبه ابزارهای گوناگون، تقریبا هر کاری را در زمینه برنامه نویسی مهندسی امکانپذیر می سازد. علاوه بر این، سادگی برنامه نویسی به زبان متلب، موجب بکارگیری آن در شاخه ها و گرایش های مختلف علمی شده است.
|
لیست توابع مورد استفاده |
کاربرد |
|
loglog |
ترسیم نمودار با هر دو محور لگاریتمی |
|
semilogx |
ترسیم نمودار با محور لگاریتمی افقی |
|
semilogy |
ترسیم نمودار با محور لگاریتمی قائم |
|
Gcf=get corrent figure |
شماره نمودار فعال که تغییرات روی ان اعمال می شود را نشان میدهد |
|
gca |
محور فعال را نشان میدهد |
|
Get |
این تابع شماره شناسایی و یا gca,.. را می گیرد و با ان شماره تمام خصوصیات ان شی را که ان شماره شناسایی را دارد استخراج میکند و یا تمام چیزها را در مورد اخرین فراخوانی gca میدهد ( محتویات و خصوصیات شی فعال را نشان می دهد ) |
|
set |
خصوصیات گرفته شده از تابع get را با این تابع می توان تغییر داد |
|
pie |
ترسیم نمودارها دایروی بر حسب درصد |
|
randn |
تولید عداد تصادفی نرمال با انحراف معیار تقریبا ۱ ( استاندراد ) و میانگین تقریبا ۰ |
|
unifrand |
یک سری اعداد بین بازه min , max می خواهم داشته باشم که توزیع یکنواخت داشته باشد و نه نرمال که تولید میکند |
|
randi |
تولید یک سری از اعداد صحیح بین min , max با توزیع یکنواخت |
|
rand |
سری از اعداد که تنها بطور یکنواخت در بازه ۰ تا ۱ توزیع شده اند و نه با توزیع نرمال |
|
hist |
رسم نموار هیستوگرام + بدست اوردن مرکز دسته ها و فراوانی انها |
|
histfit |
رسم نمودار هیستوگرام و فیت نمودار بر ان |
|
Bar , barth |
هر دو برای رسم نمودار میله ای . اولی در حالت افقی و دومی در حالت قائم |
|
stairs |
رسم نمودار پله ای |
|
meshgrid |
دستوری برای تولید دیتا برای ترسیم ۳ بعدی ( ماتریس های هم بعد به ازای تمام حالات تغییر دو متغیر ایجاد میکند و بعد با انها شبکه می سازد میتوان به ازای این نقاط تابعی را کشید و یا با نقط دلخواه در ابعادی که شبکه تولید شده و با دانستن اصول ارتباط این نقط در ماتریس ها ( مثلا ضرب نقطه به نقطه یعنی درایه ها ی نظیر به نظیر در ماتریس به هم ضرب می شوند ) |
|
surf |
دستور ترسیم سطح ۳ بعدی |
|
mesh |
دستور ترسیم سطح ۳ بعدی |
|
shading |
دستور ترسیم سطح ۳ بعدی |
|
contur |
دستور ترسیم خطوط کنتر |
|
Contur3 |
دستور ترسیم خطوط کنتر ۳ بعدی |
|
Surfc, meshc |
دستور ترسیم سطح ۳ بعدی با ترکیب کنتر |
|
Ezplot,ezsurf |
دستورات ترسیم راحت ۲ و ۳ بعدی که با گرفتن معادله ترسیم را انجام می دهد و نیازی به تولید دیتا ندارد و کنترل کمی روی ان هست . |
مثال ۱: تابع سینوسی زیر را میکشیم و ترسیمات مختلفی روی ان انجام می دهیم

یک تابع سینوسی میرا بدست می آید:
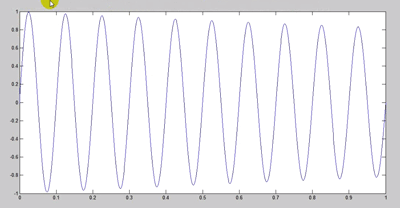
اگر ضریب قسمت نمایی را بیشتر کنیم سریعتر میرا می شود:
![]()
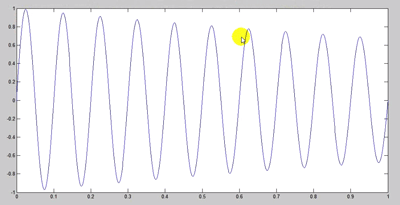
اگر باز هم زیادتر کنیم بیشتر میرا میشود:
![]()
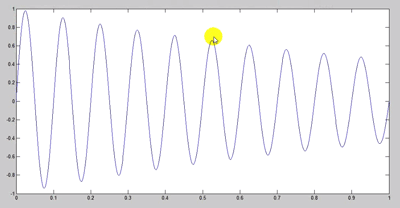
با نگه داشتن shift از قسمت workspace هر دو متغیر تولید شده t, x را انتخاب میکنیم:
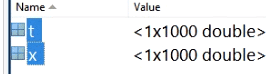
در منوی بالای صفحه قسمت plot باز می شود و t,x را در گوشه سمت چپ نشان می دهد که می توان جای آنها را هم عوض کرد. ابزارهای مختلف ترسیم را داریم مثلا plot و یا bar که با کلیک روی ان نمودار را می کشد و دستورش در command window نوشته می شود.
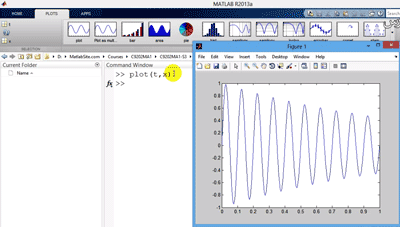
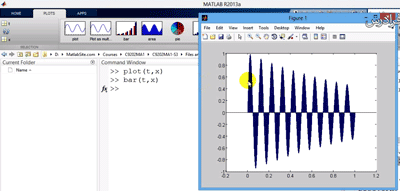
حتی می توان یکی از متغیرهای x یا t را از workspace انتخاب کرد و نمودارهای تکی برای آن کشید. در نمودارهای میله ای گاهی که تعداد داده ها زیاد است نمودار وضوح کافی ندارد می توان با بزرگنمایی قسمت کوچکی از نمودار تغییرات بار یا پله ای را بهتر دید. و یا نمودار را برای وضوح بیشتر در برنامه ای جدا برای بازه محدودی از داده ها ترسیم کرد.
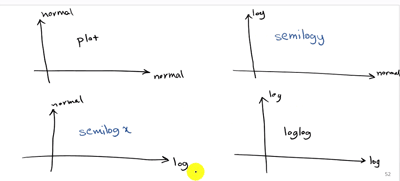
ما ۴ نوع دستور داریم اگر بخواهیم هر دو محور برای ما به صورت نرمال مقیاس بندی شود دستور plot را داریم اگر بخواهیم هر دو محورمان لگاریتمی باشد ( یعنی محورها به صورت نمایی افزایش پیدا می کنند ) به عبارتی اگر Scale تغییرات یک متغییری لگاریتمی باشد سعی می کنند محور مربوط به ان را لگاریتمی مدرج کنند که دستور متلب آن loglog هست.
دو نوع نمودار دیگر هم داریم که نیمه لگاریتمی هستند و دستور متلب آنها semilog هست که بسته به محور لگاریتمی x و y می گیرد.
به طور مثال تغییرات t را برحسب x نمایی می کنیم:
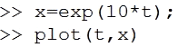
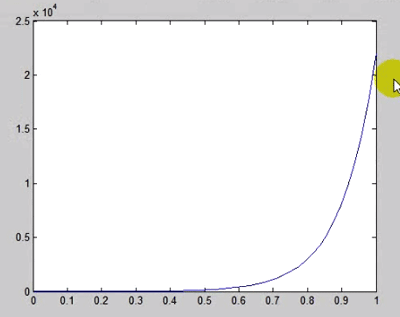
این طور توابع به سرعت افزایش پیدا می کنند ( به سرعت و با مقادیر بزرگ به سمت بینهایت می روند ) پس به ناچار در هنگام استفاده از محورهای نرمال با دستور plot ما بخش زیادی از اطلاعات را در مورد نحوه تغییرات و اعداد نمودار از دست می دهیم. کاری که باید انجام شود این است که چون محور قائم ما لگاریتمی است یعنی تغییرات نمایی دارد ان محور را لگاریتمی کنیم. پس نموداری که به صورت بالا رسم شده را edit میکنیم و محور قائم را لگاریتمی انتخاب میکنیم و نه نرمال به صورت زیر و همانطور که دیده می شود تبدیل به خط می شود یعنی این نمودار در فضای نیمه لگاریتمی یک خط است:

اگر بدون ویرایش نمودار رسم شده بخواهیم از اول نمودا فوق را نیمه لگاریتمی رسم کنیم از تابع زیر استفاده می کنیم:
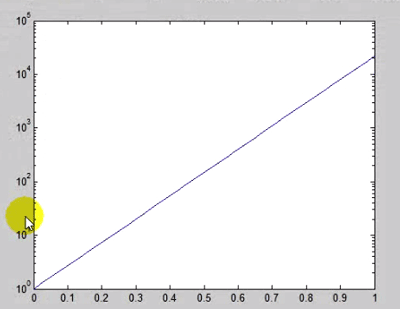
حال اگر بخواهیم هر دو محور را لگاریتمی کنیم از تابع زیر استفاده می شود باز به شکل نمایی در می آید و خطی نیست:
![]()
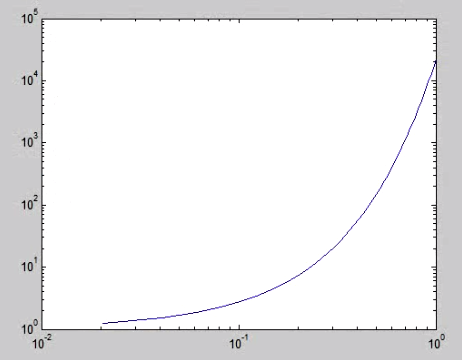
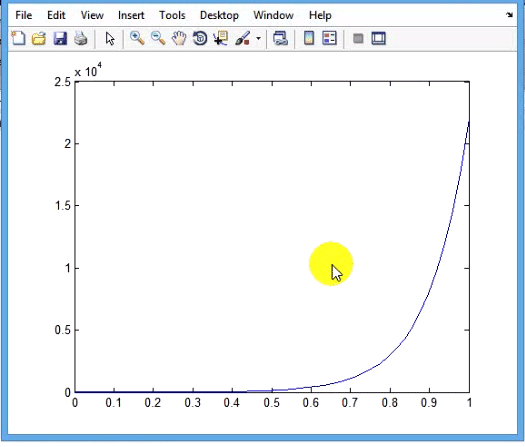
اگر محور افقی را که تغییرات نمایی ندارد لگاریتمی کنیم با دستور زیر، نمودار حاصل فوق نمایی می شود یعنی تغییرات خیلی سریع و بزرگتری به سمت بی نهایت نشان می دهد:
![]()
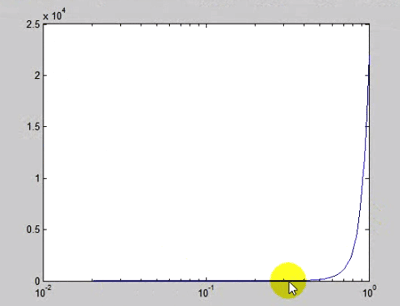
ولی بهترین حالت همان حالتی است که نمودار خطی با لگاریتمی کردن محور قائم که تغییرات نمایی دارد بدست اوردیم . زیرا وقتی با تابع plot نمودار را رسم میکنیم در روی محور قائم در ابتدای بازه زمانی چون تغییرات خیلی ناچیز است همانطور که در نمودار نیمه لگاریتمی خطی دیده می شود بازه بین ۰ تا ۱۰ همان اندازه بین بازه ۱۰ تا ۱۰۰ است و به این ترتیب رزولوشن را در روی محور قائم در زمانهای اولیه افزایش میدهد تا اطلاعات را از دست ندهیم.
با تابع زیر می توان نمودار مساحت را ترسیم کرد:
![]()
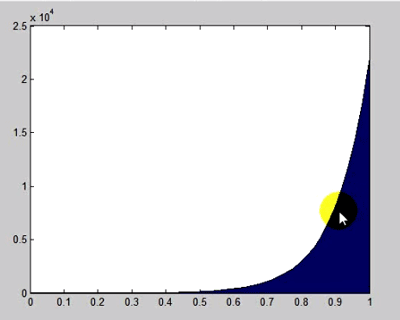
برای نیمه لگاریتمی کردن این نمودار هم می توانیم ان را edit کنیم و برای اینکه نتیجه را درست نشان دهد باید baseline=1 قرار دهیم:
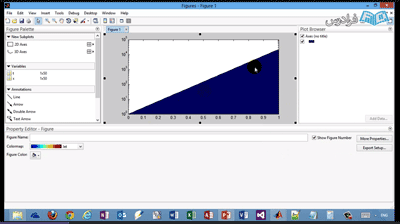
برای هر چیزی که ترسیم می شود متلب و هر برنامه ای مانند ورود یک شماره شناسایی اختصاص می دهد که مثلا اعدادی که با gca , gcf استخراج میشود شماره شناسایی آن است که با گرفتن آن شماره توسط تابع get می توانیم تمام خصوصیات ان شی مورد نظر که مثلا می تواند نمودار باشد را بدست آوریم مانند:
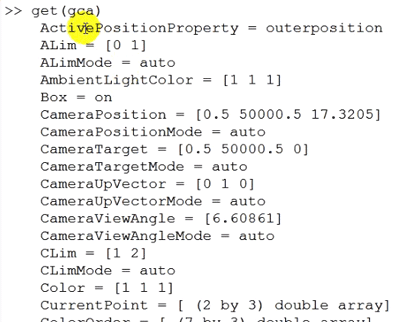
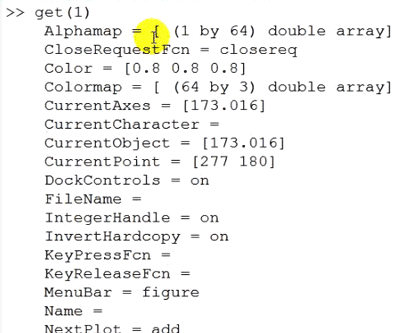
اینجا شماره آن نمودار فعال است که با تابع gcf استخراج شد و خاصیت های آن نمودار را نشان می دهد و با تابع زیر می توانیم خاصیت های محور فعال را ببینیم البته از قبل gca, gcf فراخوانی شده اند یکبار.
با دستور زیر می توانیم این خاصیت را تغییر دهیم: یعنی مثلا محور قائم را درجه بندی نرمال کرد:
![]()
با دستور زیر می توانیم این خاصیت را تغییر دهیم. یعنی مثلا محور قائم را درجه بندی نرمال کنیم:
![]()
و یا به صورت زیر لگاریتمی کنیم:
![]()
هر چیز فعالی را می توان با get خصوصیاتش را دریافت کرد و با set می توان انها را تغییر داد. با این دو تابع کارهای جالب زیادی می توان انجام داد اینجا تنها به یک مورد اشاره شد.
با دستور get می توان خصوصیتی که میخواهیم را فقط ببینیم:

با رسم نمودار پس زمینه توسی است می توان تابع gcf را فراخوانی کرد و با تابع زیر پس زمینه را سفید کرد
![]()
و کلا هر راهنمایی که در مورد این لیست و اعضای آن بخواهیم بدانیم در help متلب می توان دید.
اگر تنها یک متغیر داشته باشیم و دستور ترسیم دهیم آن را بر حسب تعدادش ترسیم می کند:

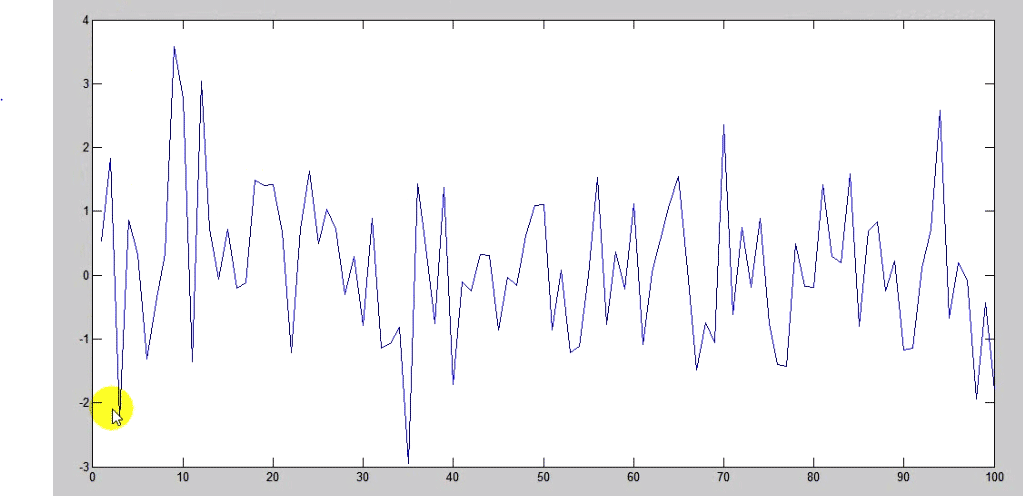
که در نمودار بالا محور افق تعداد از ۱ تا ۱۰۰و محور قائم مقادیر x است که در بازه ۱ تا ۱۰۰ مقادیر نرمال گرفته ولی به تعداد ۱۰۰ عدد گرفته. یعنی ۲ دستور زیر معادل هم هستند وقتی با عنصر اول در plot دوم تنها میخواهیم تعداد را مشخص کنیم بدن اینکه دو محور ارتباط معادلهای باهم داشته باشند. محور افق تنها شمارنده است.
وقتی هر پارامتر ترسیمی غیر از plot را با یک متغیر رسم میکنیم در واقع انگار مولفه دوم را داده ایم و مولفه اول همان از ۱:n هست و شمارنده هست.
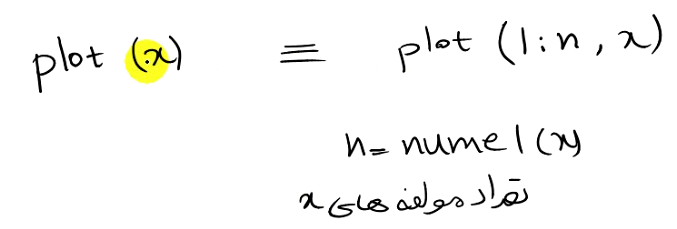
مثلا :

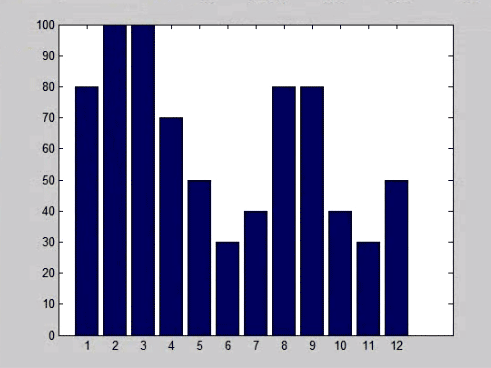
که می توان ان را ویرایش کرد مثلا محورهایش اسم بگیرند و یا تاریخ بگیرند (در مثال بالا فرض شد که x میزان بارش در هر ماه است). محور افق در واقع هیچ نیست جز شمارنده

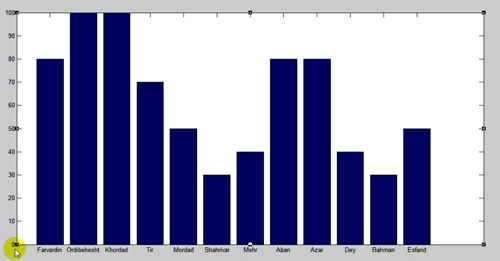
که می توان جهت انها را هم مثلا مورب کرد
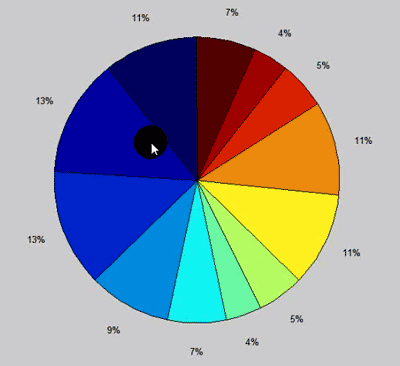
نمودارهای پای نمودارهای دایروی: 
در واقع درصد ها را نشان میدهد مثلا برا ی x در بالا که نشان دهند بارندگی بود در صد هر ماه را میدهد و می توان مقایسه کرد. مثلا ۱۱% سالانه در فروردین است و…. که اگر بخواهیم رنگ بندی ان را عوض کنیم از colormap استفاده می کنیم که با زدن doc آن می توان طیف رنگ های تعریف شده در آن را دید و انتخاب کرد مثلا:
مشابه با پای یک پای ۳ هم داریم که ۳ بعدی است:
![]()
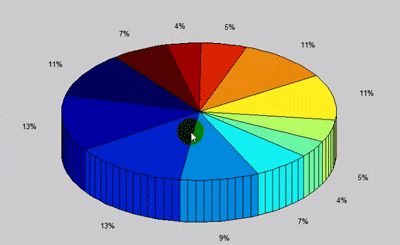
که می توان ویرایش شود . برای نوشتن اسامی محور ها می توان روی آن نام دابل کلیک کرد:
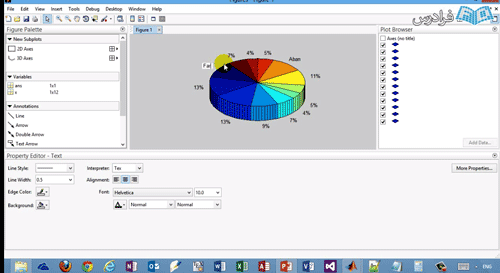
در بعضی از نمودارها می خواهیم یک قاچ از این نمودار را بیرون بکشیم مثلا در همان x بالا می خواهیم مهر ماه را بیرون بکشیم explode کنیم به ترتیب زیر عمل میکنیم که یک بردار برای explode کردن (استخراج کردن) می سازیم و ماه مورد نظر را ۱ میگیریم و بقیه صفر flage هستند تنها ان جمله درست است برای بیرون کشیدن مثلا در حالت زیر مهرماه (عضو ۷ ماتریس e را ۱ می گیریم)



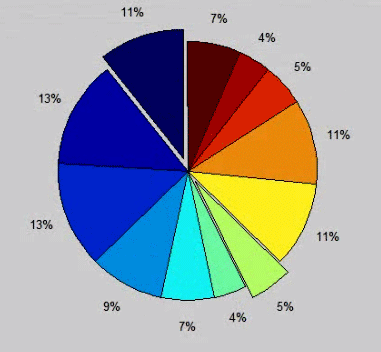
و یا می توانیم به صورت زیر عمل کنیم گفتیم که در واقع flage تعریف میکنیم: در حالت عادی هیچ چیز explode نیست با دادن دستور false یعنی همه نادرست هستند. انگار یک شرطی داریم که در ابتدا می گوئیم همه آن را نقض میکنند (هیچ تکه ای بیرون کشیده نمی شود) و بعد جملات ۷ و ۲ را تغییر میدهیم و می گوئیم true باشند در ابتدا false هستند بعد دستور pie بررسی می کند کدام جمله برای explode شدن درست است.
.هست از نظر عددی این مقادیر را دارند False=0 و true=1


:اینطور هم می توان داد

فرض میکنیم یکسری اعداد تصادفی با توزیع نرمال تولید کنیم و نمودار آن را می کشیم: تابع زیر کارش تولید اعداد تصافی نرمال استاندارد است همانطور هم که دیده می شود انحراف معیار نزدیک ۱ است.
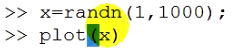

:مشخصه های آماری این توزیع نرمال را می خواهیم بدست آوریم
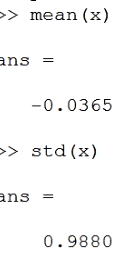
:برای دیدن هیستوگرام این اعداد
![]()
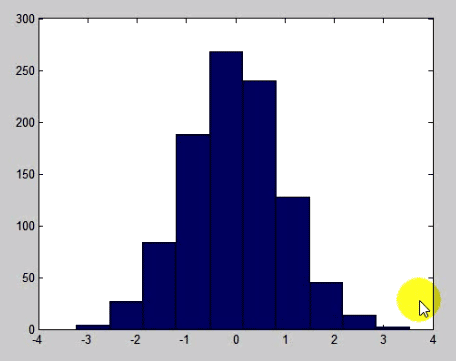
می توان بهتر نمایش داد با تعریف تعداد دسته ها که اینجا ۵۰ تا است.
![]()
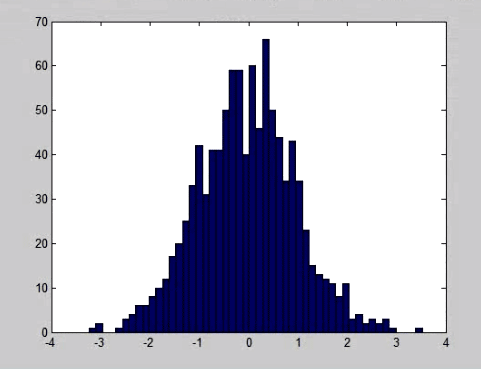
:حال اگر تعداد نقاط را زیادتر تعریف کنیم شکلی که برای توزیع نرمال وجود دارد بهتر نمایان می شود
![]()
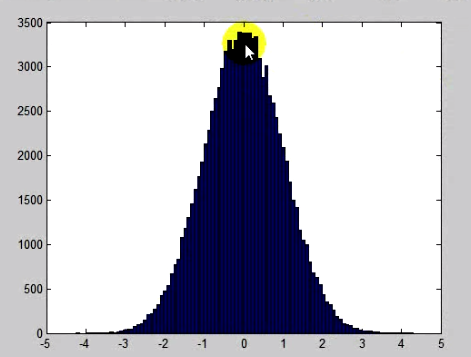
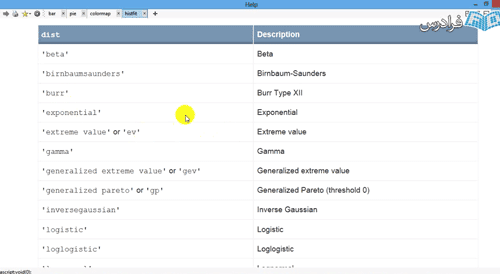
که اگر doc این تابع را باز کنیم انواع نمودارهایی که می تواند فیت کند البته هر کدام شرایطی دارند را نشان می دهد:
تابع hist تنها نمودار ترسیم نمیکند می توان از آن خروجی هم گرفت. به طور پیش فرض تعداد دسته ها را ۱۰ می گیرد و زمانی که برای گرفتن مقدار از آن استفاده میکنیم “فراوانی” هر دسته را به ما می دهد.
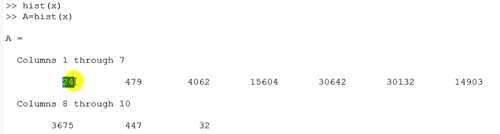
خروجی دیگری هم که دارد مرکز هر دسته است که اگر به صورت زیر فراخوانی شود انها را به ما می دهد ولی چون از رویکرد یکنواخت استفاده میکند خیلی جالب نیست این مراکزی که میدهد. ولی اگر کسی از برنامه های خوشه بندی استفاده میکند میتواند این مراکز را به ان برنامه بدهد ان برنامه این مراکز را اصلاح کند و بعد با آن ها یک هیستوگرام درست بکشد:
تابع bar نمودار میله ای قائم میدهد و تابع barth همان نمودار را به صورت افقی ترسیم میکند.
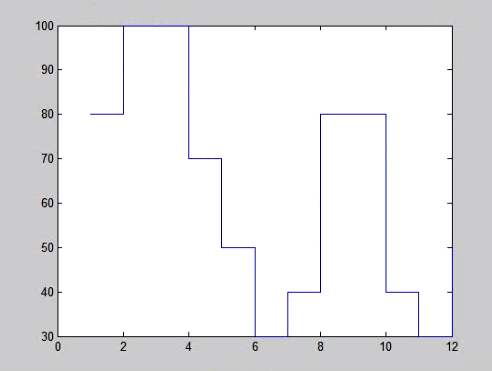
:رسم نمودار پله ای
![]()
اگر بخواهیم یک سری اعداد تولید کنیم که میانگین m و واریانس σ۲ داشته باشیم سری فوق را با m جمع می بندیم و به مقدار واریانس مورد نظر ضرب میکنیم زیرا یک توزیع نرمال را اینطور بدست می آورند بصورت زیر:
علامت ۳ تا مساوی را بکار برده برا ی ” معادل بودن “

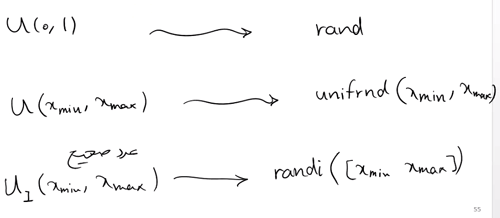
سری از اعداد می خواهیم که تنها بطور یکنواخت در بازه ۰ تا ۱ توزیع شده باشند و نه توزیع نرمال این را با rand تولید می کنند. و یا باز یک سری اعداد بین بازه min , max خودم می خواهم داشته باشم که توزیع یکنواخت داشته باشد و نه نرمال از تابع unifrand استفاده می کنیم و یا برا ی تولید یک سری از اعداد صحیح بین min , max خودم با توزیع یکنواخت از تابع randi استفاده میکنیم بصورت تصویر زیر که ابتدا مقدار min , max بازه مورد نظر خود را وارد می کنیم و بعد مقدار باید بدهیم مثلا یک ماتریس ۱۰*۱۰ می خواهم در ادامه این باید داده شود و بعد دستور را ببندیم.
گرافیک ۳ بعدی :
مثال: فرض کنید می خواهیم نمودار زیر را رسم کنیم:
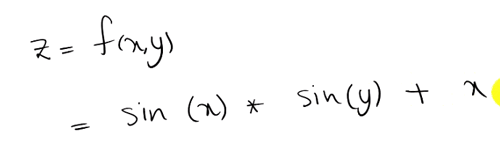
اگر فرض کنیم x 20 تا عدد و Y 30 تا عدد بگیرد در کل ۶۰۰ ترکیب بین این دو می توان ایجاد کرد برا ی این کار از تابع زیر استفاه می شود . برا ی مثال ساده زیر ۶ حالت بین این دو متغییر وجود دارد و با تابع زیر دو ماتریس که هر کدام ۶ عضو دارند و ابعاد برابر دارند هر دو ۲*۳ هستند را ایجاد می کنیم یعنی تمام حالت های ممکن (۱و۴، ۱و۵، ۲و۴، ۲و۵، ۳و۴، ۳و۵) را به ما داده باید این دو را روی هم گذاشت یعنی این زوج ها را ایجاد کرد:
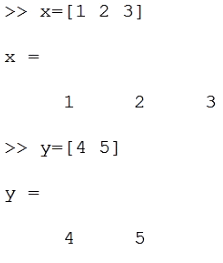

درمثال گفته شده و برای ۶۰ حالت بین این دو متغییر داریم: چون هر دو X,Y تولید شده ماتریس هستند (ماتریس از حالت های مختلف ترکیب دو متغیر اولیه هستند پس ضرب ماتریسی می شوند (که دقیقا جفتهای ایجاد شده از ترکیب حالت های مختلف دو متغیر اولیه به هم ضرب می شوند) )

![]()
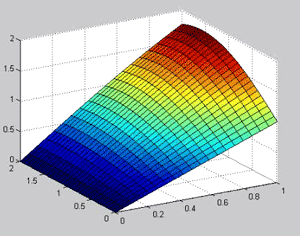
(اگر تعداد نقاط را زیادتر کنیم به سطح مورد نظر ما نزدیک تر می شود.(دقت زیادتر

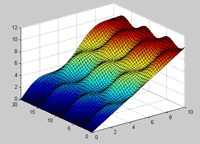
.می کند hot دستور زیر طیف رنگ را عوض می کند مثلا
![]()
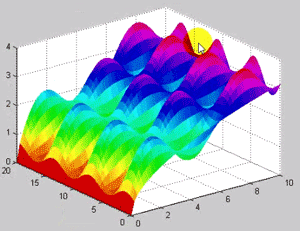
:دستور دیگر برا ی ترسیم سطح ۳ بعدی با دستورزیر است

![]()
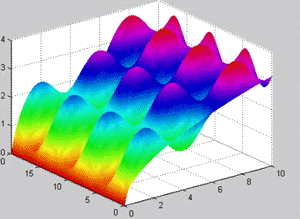
دستور سطح دیگر وجود دارد که در واقع درون یابی می کند و تغیرات را به صورت نرم تر نشان می دهد:
![]()
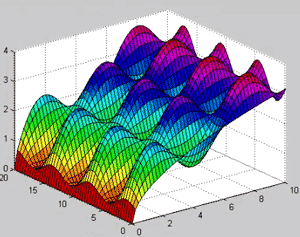
:وجود دارد shading و باز دستو دیگری در این
![]()
انواع نمودارهای ۳ بعدی را می توان در help متلب دید:

به عنوان مثال ترسیم تابع بالا با دستور mesh:

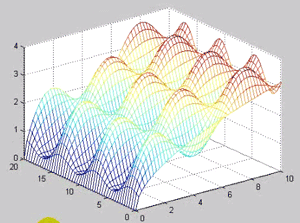
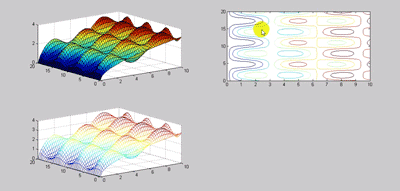
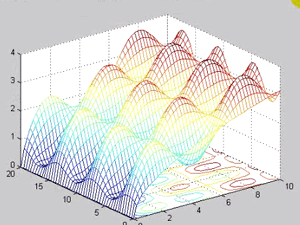
:نوع دیگری داریم که نمودار ۲ بعدی است ولی مفهومی که از ان برداشت می شود ۳ بعدی است که همان نمودارهای کنتوری هستند

:که همان شکل ۳ بعدی است ولی سطوح کانتوری ان را برای ما ترسیم کرده
![]()
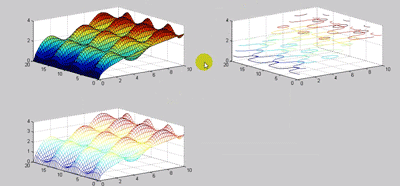
که در دستور کانتور می توان تعداد level هایی که می خواهیم ترسیم شود را معلوم کرد که مثلا در حالت زیر ۳ level را ترسیم می کند: که باز برای ۳ contour هم می توان level تعریف کرد اگر به نمودار ۳ بعدی از بالا نگاه کنیم این کانتورها رادر ۲ بعد نشان میدهد (با دوران شکل)

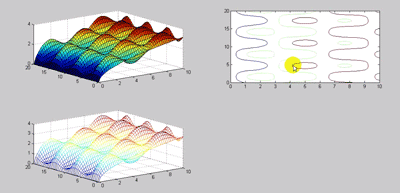
:حالت ترکیب کانتور با سطح را میتوان با دستور زیر بدست آورد

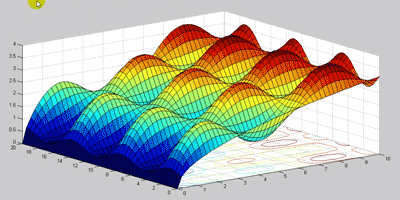

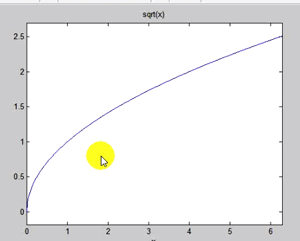
یک دسته توابعی هستند که با ez شروع می شوند که مثل همان easy تلفظ می شود و هر تابعی که در ابتدای آن این مخفف موجود دارد همان تابع مربوطه است ولی کار کردن با این نوع راحت تر است یک تابع می گیرد و آن را رسم میکند که معادله درون آن باید رشته ای تعریف شود . خودش معادله را حل میکند و ترسیم می کند.

![]()
![]()
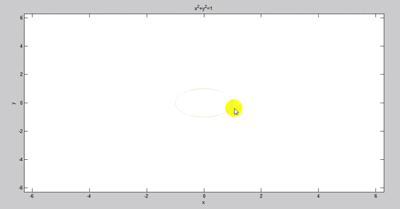
ولی این تابع عملگرهایی مثلا برای تغییر رنگ و تغییر مشخصات نمودار تولیدی ندارد باید از دستوراتی مانند set استفاده کرد. برای این منظور مشخصه یا handel و یا شناسه نمودار ایجادی را در یک متغییری میریزیم و بعد با استفاده از ان تغییرات را انجام میدهیم:
یا مثلا برای ترسیم سطح هم ez داریم و در اینجا تنها معادله را میدهیم و نیازی به تولید مختصات های جفت نیست یعنی نیازی به تولید دیتا ندارد ولی با وجود راحتی خیلی کنترل زیادی روی این نمودارها نداریم:
![]()
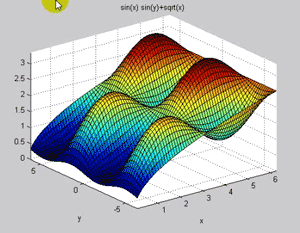
در کل توابع زیادی با ez داریم که همه عین هم هستند در نحوه فراخوانی و از این نظر تفاوتی ندارند در اینجا تنها به چند نمونه اشاره شد.
مجموعه: اخبار و تازه ها




 (No Ratings Yet)
(No Ratings Yet)